2,090 읽음
대수학의 아버지 ‘알콰리즈미’와 피보나치 수열의 ‘피보나치’를 찾아서!
 길벗
길벗 0
0지난 시리즈에서 등장한 유휘와 히파티아의 이야기는 즐겁게 보셨을까요?
수학 소설이라는 낯선 이름에도 독자분들이 주시는 애정에 힘입어
≪매스매틱스 3 : 알콰리즈미, 피보나치 편≫으로 돌아왔습니다!



네, 맞습니다! 바로 방정식과 근의 공식이죠!
이 수식들은 오늘 에피소드의 주인공,
알콰리즈미에 의해 알려졌습니다.
그의 또 다른 이름은 대수학의 아버지로 탄젠트 함수와 미지수를 최초로 인지한 위대한 수학자이기도 한데요,
오늘은 일차방정식과 이차방정식의 해법을 전해준 알콰리즈미와 함께
《매스매틱스 3》으로 시간여행을 떠나볼까요?
[줄거리]
‘유휘’와 ‘히파티아’의 시대를 그린 2권에 이어 3권에서는 대수학의 아버지라 불린 ‘알콰리즈미’와 서양에 동양 수학을 전파한 ‘피보나치’의 시대로 시간여행을 떠난 주인공의 이야기를 그렸다. 계속 변화하는 장소와 이름이지만 매 순간 헤어진 서연이를 만나기 위해 주인공은 앞으로 나아가는데…. 난해한 암호를 해독하라는 미션을 받은 그의 앞날은!?
에피소드 5(알콰리즈미 편)에서는 수학적 지식을 이용한 암호 해독과 그 과정에서 인지하는 수학과 생활의 밀접한 관련성을, 에피소드 6(피보나치 편)에서는 피보나치가 서양에 동양 수학을 전파하는 과정을 재미있는 이야기로 한 권에 담았다. 다양한 수학자를 만나는 시간여행 속에서 과연 그는 서연이를 만날 수 있을까?
(※ 본 내용은 사실이 아닌 허구로 창작된 이야기입니다.)
※ 여기서 잠깐!
에피소드 5에 등장하는 ‘알콰리즈미’는 누구일까?

그는 《힌두 수에 의한 계산법(Algoritmi de numero Indorum)》과 《이항과 소거에 의한 계산 이론(Kitab A1-mukhasar fi hisab A1-jabra wa’1 muqubala)》이라는 저서를 통해 수학적 지식을 전달하는 역할을 했으며, 최초로 탄젠트 함수 표를 작성한 인물이자 미지수를 하나의 수로 인식한 최초의 인물이기도 합니다.
그렇다면 에피소드 6에 등장하는 피보나치 수열의 ‘피보나치’는 누구?

아하! 그럼 ‘피보나치 수열’이란?
"한 쌍의 토끼로부터 일 년에 몇 쌍의 토끼가 태어날까?"
어떤 사람이 밀폐된 어떤 장소에서 암수 한 쌍의 토끼를 키운다. 첫째 달에 암컷 토끼가 암수 한 쌍의 새끼를 배고 둘째 달에 낳으며 연달아서 또 암수 한 쌍의 새끼를 밴다고 할 때, 일 년 동안 총 몇 마리의 토끼가 생기는지 구하시오.
태어난 새끼들도 마찬가지로 계속해서 새끼를 낳을 테니까요.
이 문제를 그림으로 그려 보면 이러한 결과가 도출됩니다.
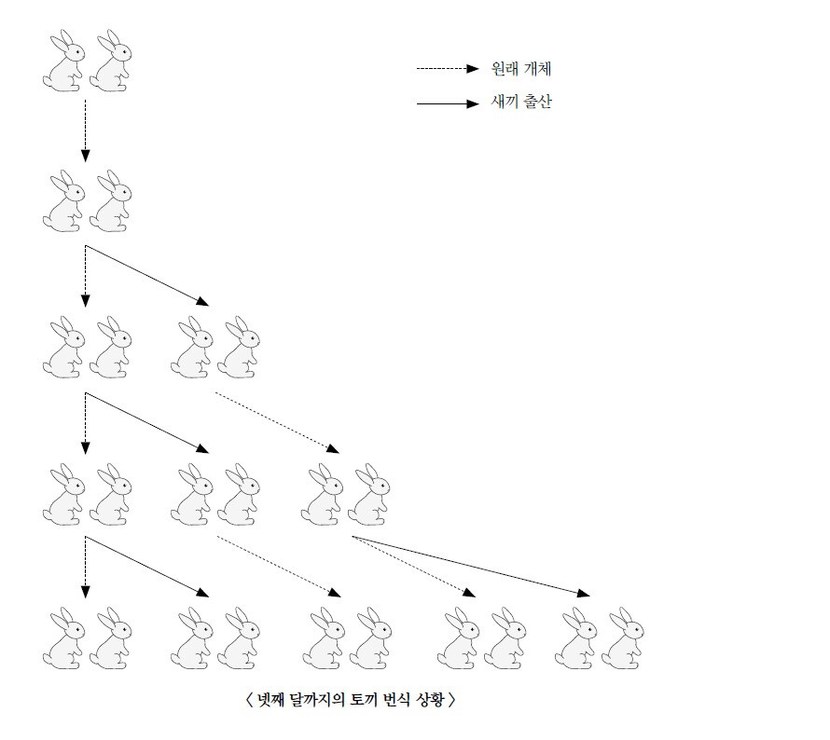
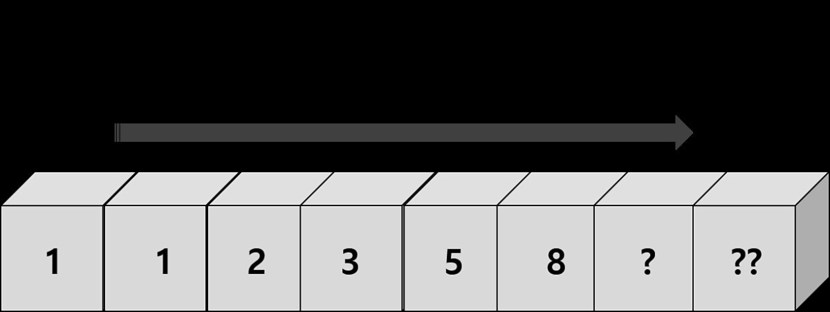
현대의 피보나치 수열은 컴퓨터 과학에서 자료 구조와 알고리즘에 최적화, 생물학에서 식물 성장의 동역학, 금융공학에서 주식 시장의 움직임을 설명하는 엘리어트 파동 이론 등 다양한 분야에서 광범위하게 활용되고 있습니다.

그 정답을 공개합니다!
? = 13
?? = 21
수학적 지식을 전부 다 이해하지 못해도 좋아요!
≪매스매틱스≫를 읽는 것만으로도 수학과 점점 가까워지는 우리를 발견할 수 있어요!
그럼 ≪매스매틱스 3≫와 함께 시간여행을 떠나볼까요?
《매스매틱스 3》은
YES24, 교보문고, 알라딘, 영풍문고에서 만날 수 있어요:)

